25. The Solow-Swan Growth Model#
In this lecture we review a famous model due to Robert Solow (1925–2023) and Trevor Swan (1918–1989).
The model is used to study growth over the long run.
Although the model is simple, it contains some interesting lessons.
We will use the following imports.
import matplotlib.pyplot as plt
import numpy as np
25.1. The model#
In a Solow–Swan economy, agents save a fixed fraction of their current incomes.
Savings sustain or increase the stock of capital.
Capital is combined with labor to produce output, which in turn is paid out to workers and owners of capital.
To keep things simple, we ignore population and productivity growth.
For each integer , output in period is given by , where is capital, is labor and is an aggregate production function.
The function is assumed to be nonnegative and homogeneous of degree one, meaning that
Production functions with this property include
the Cobb-Douglas function with .
the CES function with .
Here, is the output elasticity of capital and is a parameter that determines the elasticity of substitution between capital and labor.
We assume a closed economy, so aggregate domestic investment equals aggregate domestic saving.
The saving rate is a constant satisfying , so that aggregate investment and saving both equal .
Capital depreciates: without replenishing through investment, one unit of capital today becomes units tomorrow.
Thus,
Without population growth, equals some constant .
Setting and using homogeneity of degree one now yields
With , the final expression for capital dynamics is
Our aim is to learn about the evolution of over time, given an exogenous initial capital stock .
25.2. A graphical perspective#
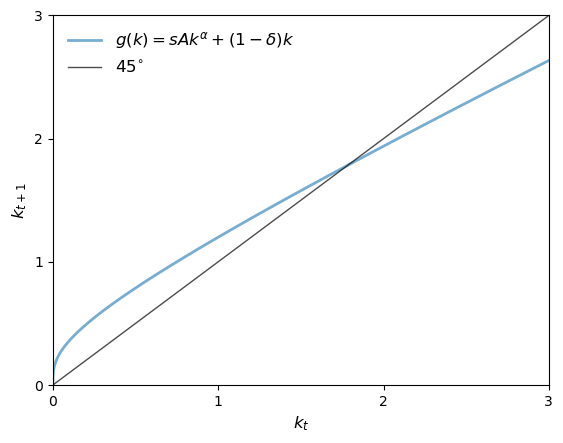
To understand the dynamics of the sequence we use a 45-degree diagram.
To do so, we first need to specify the functional form for and assign values to the parameters.
We choose the Cobb–Douglas specification and set , , and .
The function from (25.1) is then plotted, along with the 45-degree line.
Let’s define the constants.
A, s, alpha, delta = 2, 0.3, 0.3, 0.4
x0 = 0.25
xmin, xmax = 0, 3
Now, we define the function .
def g(A, s, alpha, delta, k):
return A * s * k**alpha + (1 - delta) * k
Let’s plot the 45-degree diagram of .
def plot45(kstar=None):
xgrid = np.linspace(xmin, xmax, 12000)
fig, ax = plt.subplots()
ax.set_xlim(xmin, xmax)
g_values = g(A, s, alpha, delta, xgrid)
ymin, ymax = np.min(g_values), np.max(g_values)
ax.set_ylim(ymin, ymax)
lb = r'$g(k) = sAk^{\alpha} + (1 - \delta)k$'
ax.plot(xgrid, g_values, lw=2, alpha=0.6, label=lb)
ax.plot(xgrid, xgrid, 'k-', lw=1, alpha=0.7, label=r'$45^{\circ}$')
if kstar:
fps = (kstar,)
ax.plot(fps, fps, 'go', ms=10, alpha=0.6)
ax.annotate(r'$k^* = (sA / \delta)^{(1/(1-\alpha))}$',
xy=(kstar, kstar),
xycoords='data',
xytext=(-40, -60),
textcoords='offset points',
fontsize=14,
arrowprops=dict(arrowstyle="->"))
ax.legend(loc='upper left', frameon=False, fontsize=12)
ax.set_xticks((0, 1, 2, 3))
ax.set_yticks((0, 1, 2, 3))
ax.set_xlabel('$k_t$', fontsize=12)
ax.set_ylabel('$k_{t+1}$', fontsize=12)
plt.show()
Suppose, at some , the value lies strictly above the 45-degree line.
Then we have and capital per worker rises.
If then capital per worker falls.
If , then we are at a steady state and remains constant.
(A steady state of the model is a fixed point of the mapping .)
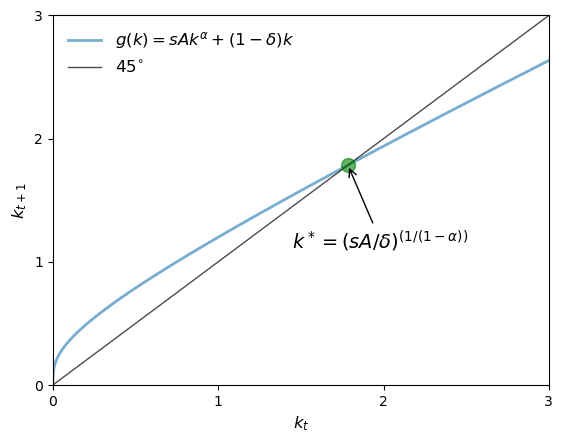
From the shape of the function in the figure, we see that there is a unique steady state in .
It solves and hence is given by
If initial capital is below , then capital increases over time.
If initial capital is above this level, then the reverse is true.
Let’s plot the 45-degree diagram to show the in the plot.
From our graphical analysis, it appears that converges to , regardless of initial capital .
This is a form of global stability.
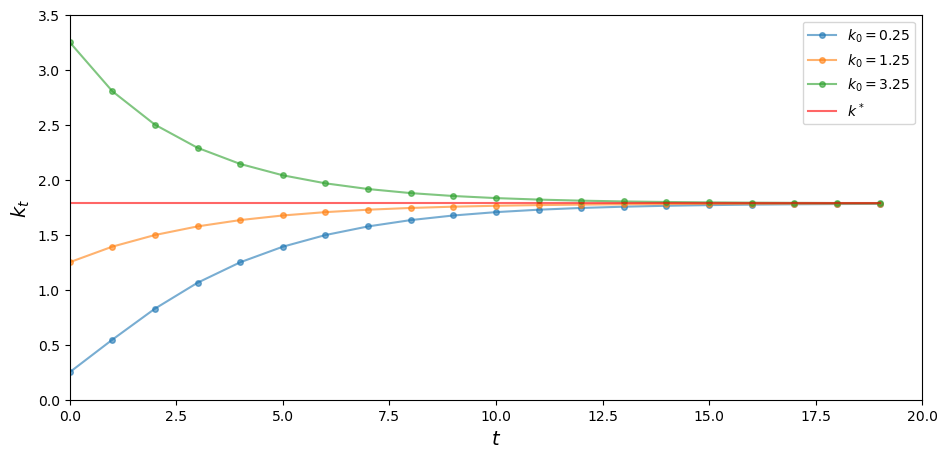
The next figure shows three time paths for capital, from three distinct initial conditions, under the parameterization listed above.
At this parameterization, .
Let’s define the constants and three distinct initial conditions
A, s, alpha, delta = 2, 0.3, 0.3, 0.4
x0 = np.array([.25, 1.25, 3.25])
ts_length = 20
xmin, xmax = 0, ts_length
ymin, ymax = 0, 3.5
def simulate_ts(x0_values, ts_length):
k_star = (s * A / delta)**(1/(1-alpha))
fig, ax = plt.subplots(figsize=[11, 5])
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ts = np.zeros(ts_length)
# simulate and plot time series
for x_init in x0_values:
ts[0] = x_init
for t in range(1, ts_length):
ts[t] = g(A, s, alpha, delta, ts[t-1])
ax.plot(np.arange(ts_length), ts, '-o', ms=4, alpha=0.6,
label=r'$k_0=%g$' %x_init)
ax.plot(np.arange(ts_length), np.full(ts_length,k_star),
alpha=0.6, color='red', label=r'$k^*$')
ax.legend(fontsize=10)
ax.set_xlabel(r'$t$', fontsize=14)
ax.set_ylabel(r'$k_t$', fontsize=14)
plt.show()
As expected, the time paths in the figure all converge to .
25.3. Growth in continuous time#
In this section, we investigate a continuous time version of the Solow–Swan growth model.
We will see how the smoothing provided by continuous time can simplify our analysis.
Recall that the discrete time dynamics for capital are given by .
A simple rearrangement gives the rate of change per unit of time:
Taking the time step to zero gives the continuous time limit
Our aim is to learn about the evolution of over time, given an initial stock .
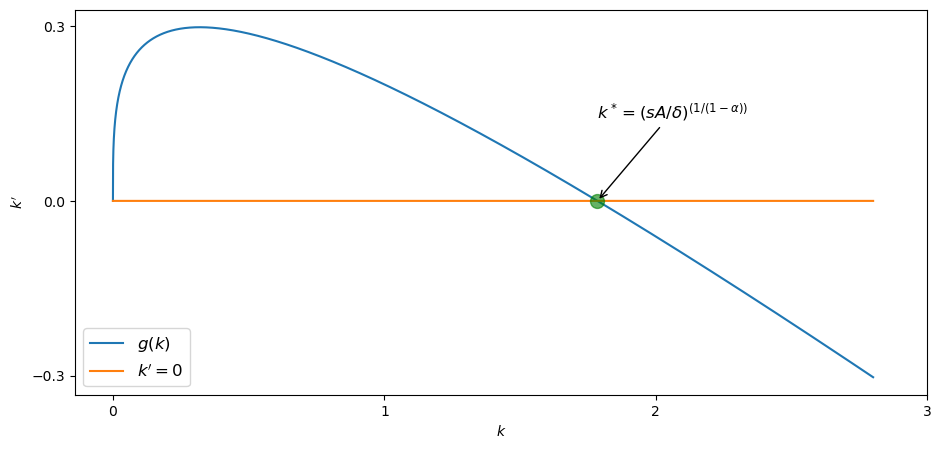
A steady state for (25.3) is a value at which capital is unchanging, meaning or, equivalently, .
We assume , so solves .
The solution is the same as the discrete time case—see (25.2).
The dynamics are represented in the next figure, maintaining the parameterization we used above.
Writing with , values of with imply , so capital is increasing.
When , the opposite occurs. Once again, high marginal returns to savings at low levels of capital combined with low rates of return at high levels of capital combine to yield global stability.
To see this in a figure, let’s define the constants
A, s, alpha, delta = 2, 0.3, 0.3, 0.4
Next we define the function for growth in continuous time
def g_con(A, s, alpha, delta, k):
return A * s * k**alpha - delta * k
def plot_gcon(kstar=None):
k_grid = np.linspace(0, 2.8, 10000)
fig, ax = plt.subplots(figsize=[11, 5])
ax.plot(k_grid, g_con(A, s, alpha, delta, k_grid), label='$g(k)$')
ax.plot(k_grid, 0 * k_grid, label="$k'=0$")
if kstar:
fps = (kstar,)
ax.plot(fps, 0, 'go', ms=10, alpha=0.6)
ax.annotate(r'$k^* = (sA / \delta)^{(1/(1-\alpha))}$',
xy=(kstar, 0),
xycoords='data',
xytext=(0, 60),
textcoords='offset points',
fontsize=12,
arrowprops=dict(arrowstyle="->"))
ax.legend(loc='lower left', fontsize=12)
ax.set_xlabel("$k$",fontsize=10)
ax.set_ylabel("$k'$", fontsize=10)
ax.set_xticks((0, 1, 2, 3))
ax.set_yticks((-0.3, 0, 0.3))
plt.show()
This shows global stability heuristically for a fixed parameterization, but how would we show the same thing formally for a continuum of plausible parameters?
In the discrete time case, a neat expression for is hard to obtain.
In continuous time the process is easier: we can obtain a relatively simple expression for that specifies the entire path.
The first step is to set , so that .
Substituting into leads to the linear differential equation
This equation, which is a linear ordinary differential equation, has the solution
(You can confirm that this function satisfies (25.4) by differentiating it with respect to .)
Converting back to yields
Since and , we see immediately that as independent of .
Thus, global stability holds.
25.4. Exercises#
Exercise 25.1
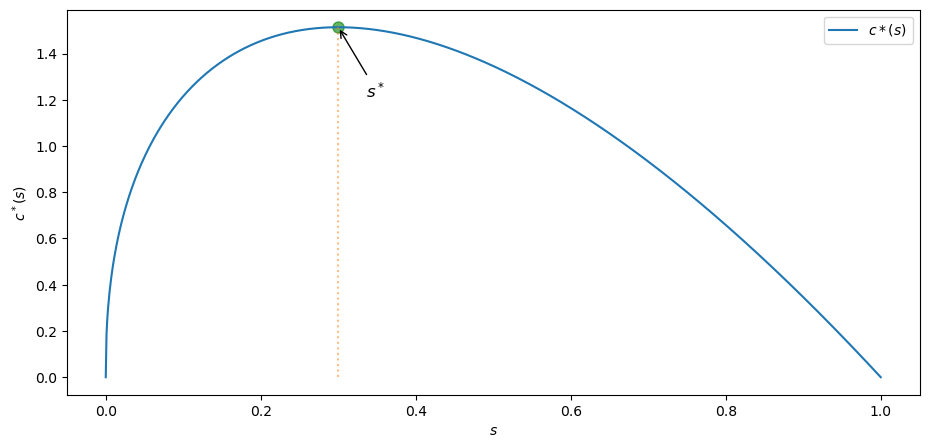
Plot per capita consumption at the steady state, as a function of the savings rate , where .
Use the Cobb–Douglas specification .
Set and
Also, find the approximate value of that maximizes the and show it in the plot.
Solution to Exercise 25.1
Steady state consumption at savings rate is given by
A = 2.0
alpha = 0.3
delta = 0.5
s_grid = np.linspace(0, 1, 1000)
k_star = ((s_grid * A) / delta)**(1/(1 - alpha))
c_star = (1 - s_grid) * A * k_star ** alpha
Let’s find the value of that maximizes using scipy.optimize.minimize_scalar.
We will use since minimize_scalar finds the minimum value.
from scipy.optimize import minimize_scalar
def calc_c_star(s):
k = ((s * A) / delta)**(1/(1 - alpha))
return - (1 - s) * A * k ** alpha
return_values = minimize_scalar(calc_c_star, bounds=(0, 1))
s_star_max = return_values.x
c_star_max = -return_values.fun
print(f"Function is maximized at s = {round(s_star_max, 4)}")
Function is maximized at s = 0.3
x_s_max = np.array([s_star_max, s_star_max])
y_s_max = np.array([0, c_star_max])
fig, ax = plt.subplots(figsize=[11, 5])
fps = (c_star_max,)
# Highlight the maximum point with a marker
ax.plot((s_star_max, ), (c_star_max,), 'go', ms=8, alpha=0.6)
ax.annotate(r'$s^*$',
xy=(s_star_max, c_star_max),
xycoords='data',
xytext=(20, -50),
textcoords='offset points',
fontsize=12,
arrowprops=dict(arrowstyle="->"))
ax.plot(s_grid, c_star, label=r'$c*(s)$')
ax.plot(x_s_max, y_s_max, alpha=0.5, ls='dotted')
ax.set_xlabel(r'$s$')
ax.set_ylabel(r'$c^*(s)$')
ax.legend()
plt.show()
One can also try to solve this mathematically by differentiating and solve for using sympy.
from sympy import solve, Symbol
s_symbol = Symbol('s', real=True)
k = ((s_symbol * A) / delta)**(1/(1 - alpha))
c = (1 - s_symbol) * A * k ** alpha
Let’s differentiate and solve using sympy.solve
# Solve using sympy
s_star = solve(c.diff())[0]
print(f"s_star = {s_star}")
s_star = 0.300000000000000
Incidentally, the rate of savings which maximizes steady state level of per capita consumption is called the Golden Rule savings rate.
Exercise 25.2
Stochastic Productivity
To bring the Solow–Swan model closer to data, we need to think about handling random fluctuations in aggregate quantities.
Among other things, this will eliminate the unrealistic prediction that per-capita output converges to a constant .
We shift to discrete time for the following discussion.
One approach is to replace constant productivity with some stochastic sequence .
Dynamics are now
We suppose is Cobb–Douglas and is IID and lognormal.
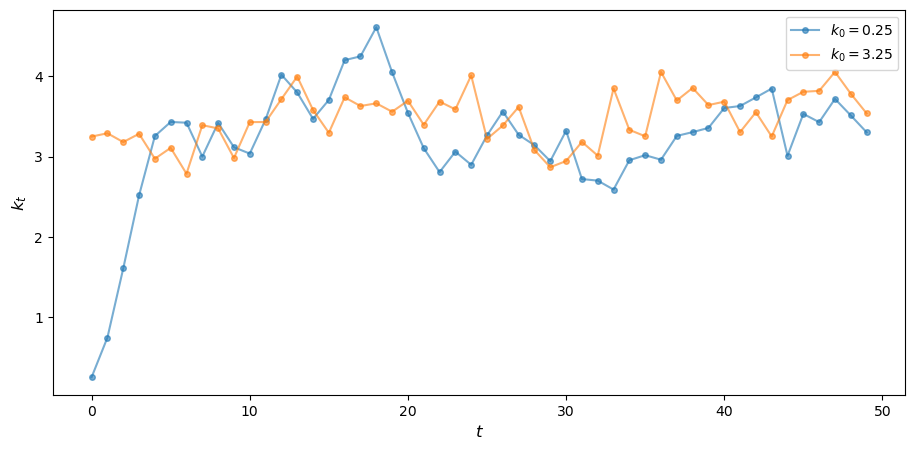
Now the long run convergence obtained in the deterministic case breaks down, since the system is hit with new shocks at each point in time.
Consider and
Generate and plot the time series .
Solution to Exercise 25.2
Let’s define the constants for lognormal distribution and initial values used for simulation
# Define the constants
sig = 0.2
mu = np.log(2) - sig**2 / 2
A = 2.0
s = 0.6
alpha = 0.3
delta = 0.5
x0 = [.25, 3.25] # list of initial values used for simulation
Let’s define the function k_next to find the next value of
def lgnorm():
return np.exp(mu + sig * np.random.randn())
def k_next(s, alpha, delta, k):
return lgnorm() * s * k**alpha + (1 - delta) * k
def ts_plot(x_values, ts_length):
fig, ax = plt.subplots(figsize=[11, 5])
ts = np.zeros(ts_length)
# simulate and plot time series
for x_init in x_values:
ts[0] = x_init
for t in range(1, ts_length):
ts[t] = k_next(s, alpha, delta, ts[t-1])
ax.plot(np.arange(ts_length), ts, '-o', ms=4,
alpha=0.6, label=r'$k_0=%g$' %x_init)
ax.legend(loc='best', fontsize=10)
ax.set_xlabel(r'$t$', fontsize=12)
ax.set_ylabel(r'$k_t$', fontsize=12)
plt.show()